publications

reports

2025

1. Oberwolfach Preprint

   

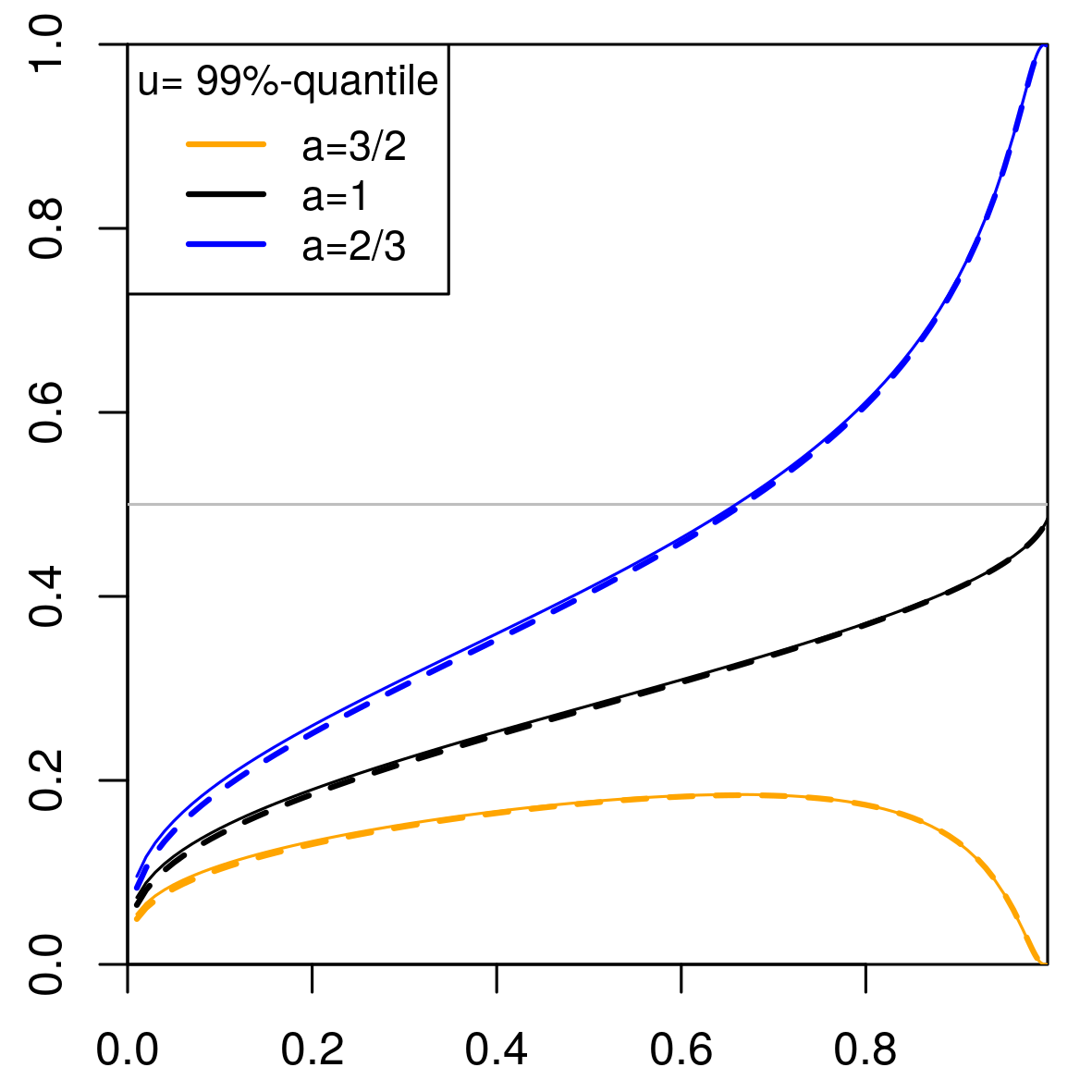   Domain-Scaled Regular Variation: Mathematical Foundations for a New Tail Process

   Kirstin Strokorb, Marco Oesting, and Raphaël Fondeville

   2025

   Abs DOI Bib

   Threshold exceedances of stochastic processes in space and time often appear to be more localized the more extreme they are. While classical regularly varying stochastic processes cannot model this effect, we introduce an adapted version of regular variation, where a suitable domain-scaling can be incorporated to accommodate this behaviour. Our theory is inspired by the triangular array convergence of domain-scaled maxima of Gaussian processes to a Brown-Resnick process and turns out to be natural in this context. We study key properties of the resulting tail process and demonstrate its ability to approximate conditional exceedance probabilities of Gaussian processes. Mathematical convenience arises from the recently rediscovered concept of vague convergence based on boundedness.

   @techreport{mfo2025domain,
     title = {Domain-Scaled Regular Variation: Mathematical Foundations for a New Tail Process},
     author = {Strokorb, Kirstin and Oesting, Marco and de Fondeville, Rapha{\"e}l},
     year = {2025},
     institution = {Mathematisches Forschungsinstitut Oberwolfach},
     doi = {10.14760/OWP-2025-02},
     series = {Oberwolfach Preprints},
     volume = {2025-02}
   }

journal articles

2025

1. AAP

   

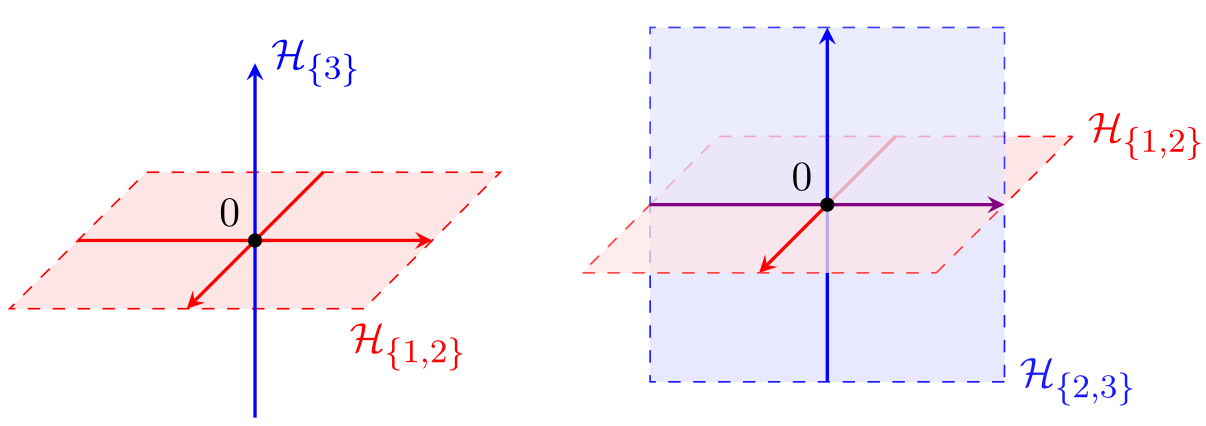   Graphical models for infinite measures with applications to extremes

   Sebastian Engelke, Jevgenijs Ivanovs, and Kirstin Strokorb

   Ann. Appl. Probab., 2025

   Abs DOI Bib

   Conditional independence and graphical models are well studied for probability distributions on product spaces. We propose a new notion of conditional independence for any measure Λon the punctured Euclidean space \mathbb R^d∖{0} that explodes at the origin. The importance of such measures stems from their connection to infinitely divisible and max-infinitely divisible distributions, where they appear as Lévy measures and exponent measures, respectively. We characterize independence and conditional independence for Λin various ways through kernels and factorization of a modified density, including a Hammersley–Clifford type theorem for undirected graphical models. As opposed to the classical conditional independence, our notion is intimately connected to the support of the measure Λ. Our general theory unifies and extends recent approaches to graphical modeling in the fields of extreme value analysis and Lévy processes. Our results for the corresponding undirected and directed graphical models lay the foundation for new statistical methodology in these areas.

   @article{graphmodelsExtremes,
     author = {Engelke, Sebastian and Ivanovs, Jevgenijs and Strokorb, Kirstin},
     title = {Graphical models for infinite measures with applications to extremes},
     volume = {35},
     journal = {Ann. Appl. Probab.},
     fjournal = {The Annals of Applied Probability},
     number = {5},
     publisher = {Institute of Mathematical Statistics},
     pages = {3490 -- 3542},
     keywords = {Conditional independence, exponent measure, Extremes, Infinite divisibility, Lévy measure, stable distribution},
     year = {2025},
     doi = {10.1214/25-AAP2201},
     url = {https://doi.org/10.1214/25-AAP2201}
   }

2024

1. Extremes

   

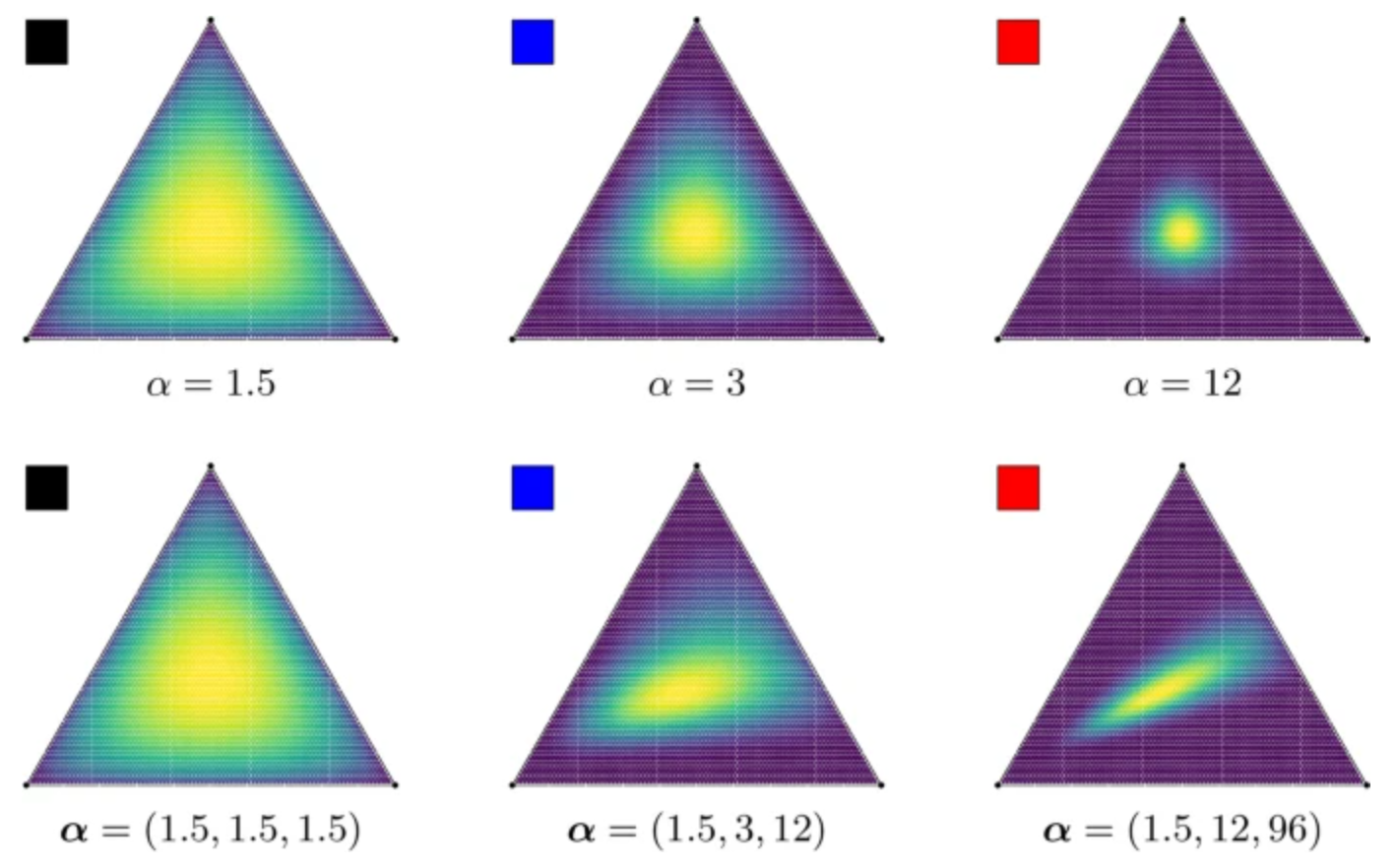   Stochastic ordering in multivariate extremes

   Michela Corradini and Kirstin Strokorb

   Extremes, 2024

   Abs DOI Bib

   The article considers the multivariate stochastic orders of upper orthants, lower orthants and positive quadrant dependence (PQD) among simple max-stable distributions and their exponent measures. It is shown for each order that it holds for the max-stable distribution if and only if it holds for the corresponding exponent measure. The finding is non-trivial for upper orthants (and hence PQD order). From dimension d≥3 these three orders are not equivalent and a variety of phenomena can occur. However, every simple max-stable distribution PQD-dominates the corresponding independent model and is PQD-dominated by the fully dependent model. Among parametric models the asymmetric Dirichlet family and the Hüsler-Reiß family turn out to be PQD-ordered according to the natural order within their parameter spaces. For the Hüsler-Reiß family this holds true even for the supermodular order.

   @article{MR4778951,
     author = {Corradini, Michela and Strokorb, Kirstin},
     title = {Stochastic ordering in multivariate extremes},
     journal = {Extremes},
     fjournal = {Extremes. Statistical Theory and Applications in Science,
                   Engineering and Economics},
     volume = {27},
     year = {2024},
     number = {3},
     pages = {357--396},
     issn = {1386-1999,1572-915X},
     mrclass = {60G70 (60E15)},
     mrnumber = {4778951},
     doi = {10.1007/s10687-024-00486-0},
     url = {https://doi.org/10.1007/s10687-024-00486-0}
   }

2. AISM

   

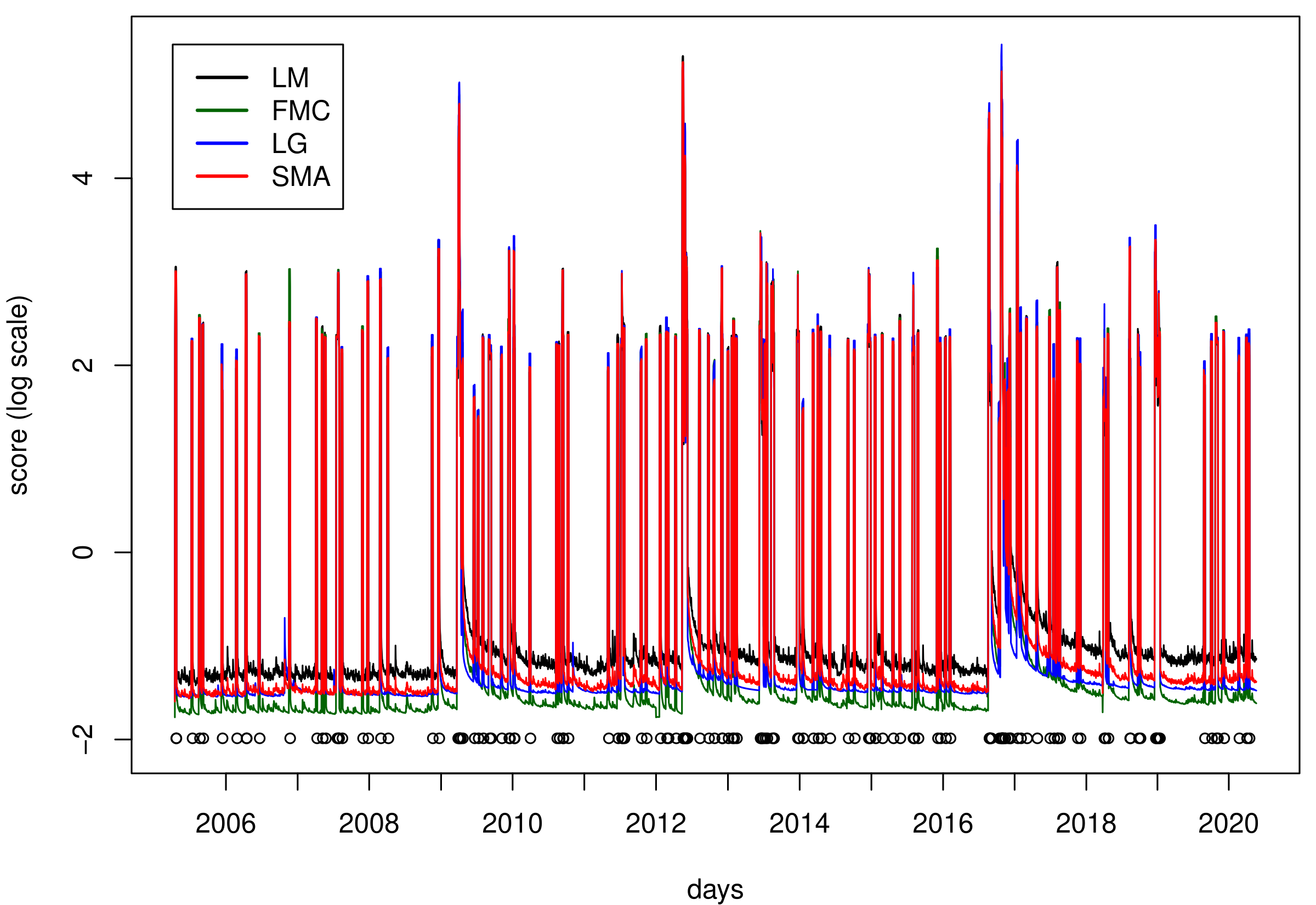   Comparative evaluation of point process forecasts

   Jonas R. Brehmer, Tilmann Gneiting, Marcus Herrmann, Warner Marzocchi, Martin Schlather, and Kirstin Strokorb

   Ann. Inst. Statist. Math., 2024

   Abs DOI Bib

   Stochastic models of point patterns in space and time are widely used to issue forecasts or assess risk, and often they afect societally relevant decisions. We adapt the concept of consistent scoring functions and proper scoring rules, which are statistically principled tools for the comparative evaluation of predictive performance, to the point process setting, and place both new and existing methodology in this framework. With reference to earthquake likelihood model testing, we demonstrate that extant techniques apply in much broader contexts than previously thought. In particular, the Poisson log-likelihood can be used for theoretically principled comparative forecast evaluation in terms of cell expectations. We illustrate the approach in a simulation study and in a comparative evaluation of operational earthquake forecasts for Italy.

   @article{MR4684016,
     author = {Brehmer, Jonas R. and Gneiting, Tilmann and Herrmann, Marcus and Marzocchi, Warner and Schlather, Martin and Strokorb, Kirstin},
     title = {Comparative evaluation of point process forecasts},
     journal = {Ann. Inst. Statist. Math.},
     fjournal = {Annals of the Institute of Statistical Mathematics},
     volume = {76},
     year = {2024},
     number = {1},
     pages = {47--71},
     issn = {0020-3157,1572-9052},
     mrclass = {62M20 (60G55 62C05)},
     mrnumber = {4684016},
     doi = {10.1007/s10463-023-00875-5},
     url = {https://doi.org/10.1007/s10463-023-00875-5}
   }

2022

1. Statist. Sci.

   

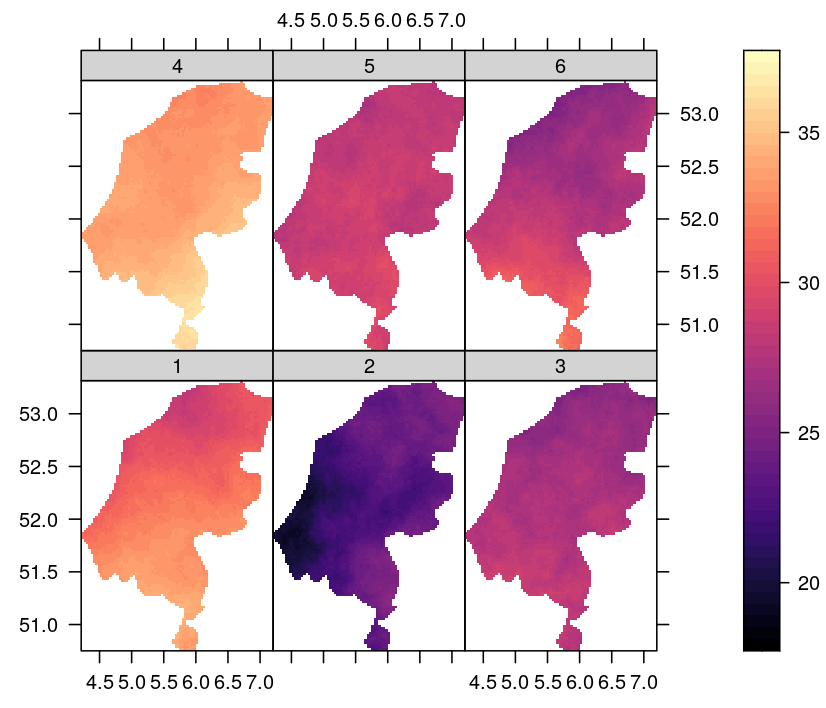   A comparative tour through the simulation algorithms for max-stable processes

   Marco Oesting and Kirstin Strokorb

   Statist. Sci., 2022

   Abs DOI Bib

   Being the max-analogue of α-stable stochastic processes, max-stable processes form one of the fundamental classes of stochastic processes. With the arrival of sufficient computational capabilities, they have become a benchmark in the analysis of spatio-temporal extreme events. Simulation is often a necessary part of inference of certain characteristics, in particular for future spatial risk assessment. In this article we give an overview over existing procedures for this task, put them into perspective of one another and use some new theoretical results to make comparisons with respect to their properties.

   @article{MR4372096,
     author = {Oesting, Marco and Strokorb, Kirstin},
     title = {A comparative tour through the simulation algorithms for
                   max-stable processes},
     journal = {Statist. Sci.},
     fjournal = {Statistical Science. A Review Journal of the Institute of
                   Mathematical Statistics},
     volume = {37},
     year = {2022},
     number = {1},
     pages = {42--63},
     issn = {0883-4237,2168-8745},
     mrclass = {99-01},
     mrnumber = {4372096},
     doi = {10.1214/20-sts820},
     url = {https://doi.org/10.1214/20-sts820}
   }

2019

1. EJS

   Why scoring functions cannot assess tail properties

   Jonas R. Brehmer and Kirstin Strokorb

   Electron. J. Stat., 2019

   Abs DOI Bib

   Motivated by the growing interest in sound forecast evaluation techniques with an emphasis on distribution tails rather than average behaviour, we investigate a fundamental question arising in this context: Can statistical features of distribution tails be elicitable, i.e. be the unique minimizer of an expected score? We demonstrate that expected scores are not suitable to distinguish genuine tail properties in a very strong sense. Specifically, we introduce the class of max-functionals, which contains key characteristics from extreme value theory, for instance the extreme value index. We show that its members fail to be elicitable and that their elicitation complexity is in fact infinite under mild regularity assumptions. Further we prove that, even if the information of a max-functional is reported via the entire distribution function, a proper scoring rule cannot separate max-functional values. These findings highlight the caution needed in forecast evaluation and statistical inference if relevant information is encoded by such functionals.

   @article{MR4015787,
     author = {Brehmer, Jonas R. and Strokorb, Kirstin},
     title = {Why scoring functions cannot assess tail properties},
     journal = {Electron. J. Stat.},
     fjournal = {Electronic Journal of Statistics},
     volume = {13},
     year = {2019},
     number = {2},
     pages = {4015--4034},
     issn = {1935-7524},
     mrclass = {62C05 (62G32 91B06)},
     mrnumber = {4015787},
     doi = {10.1214/19-EJS1622},
     url = {https://doi.org/10.1214/19-EJS1622}
   }

2018

1. Adv. Appl. Probab.

   

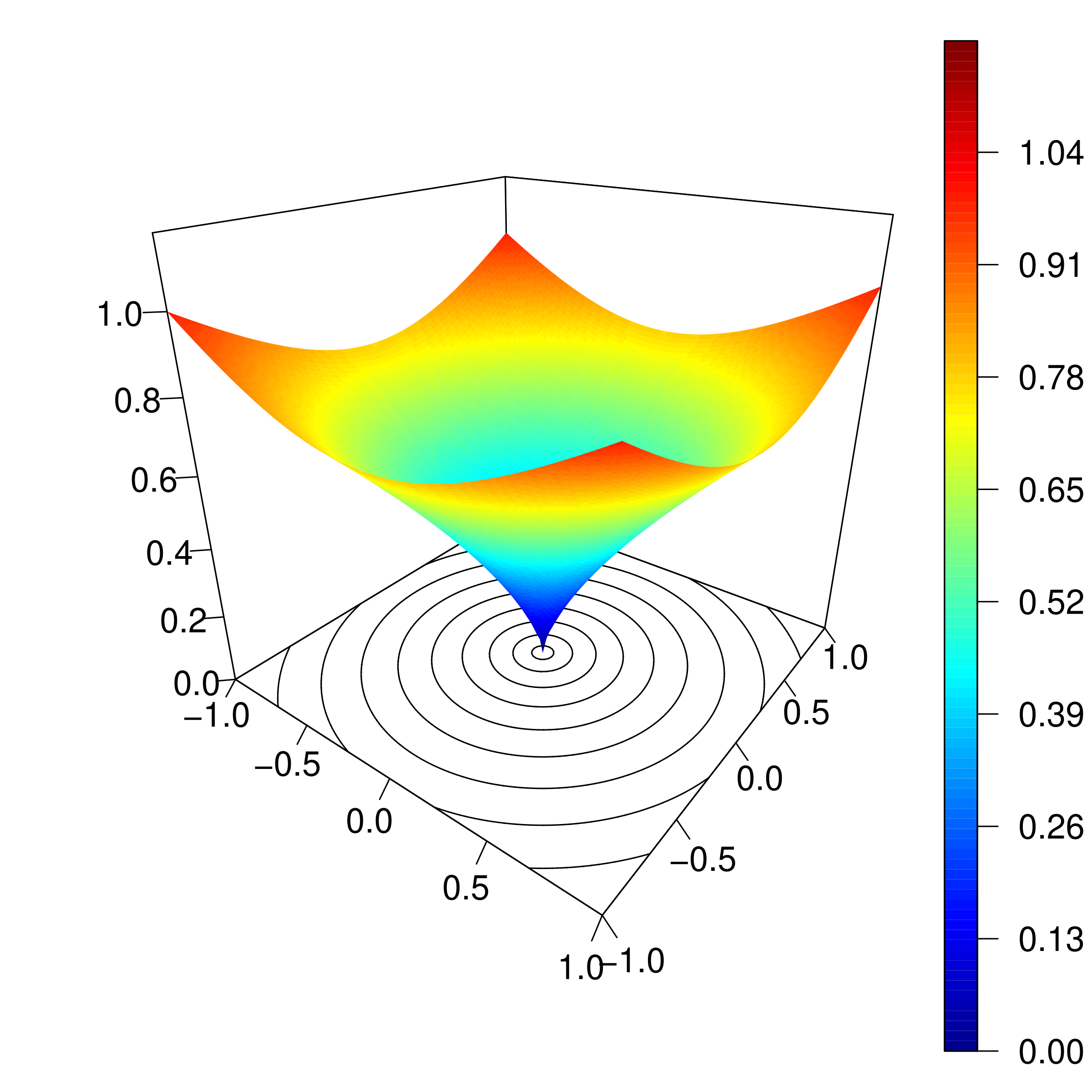   Efficient simulation of Brown-Resnick processes based on variance reduction of Gaussian processes

   Marco Oesting and Kirstin Strokorb

   Adv. in Appl. Probab., 2018

   Abs DOI Bib

   Brown-Resnick processes are max-stable processes that are associated to Gaussian processes. Their simulation is often based on the corresponding spectral representation which is not unique. We study to what extent simulation accuracy and efficiency can be improved by minimizing the maximal variance of the underlying Gaussian process. Such a minimization is a difficult mathematical problem that also depends on the geometry of the simulation domain. We extend Matheron’s (1974) seminal contribution in two aspects: (i) making his description of a minimal maximal variance explicit for convex variograms on symmetric domains and (ii) proving that the same strategy reduces the maximal variance also for a huge class of non-convex variograms representable through a Bernstein function. A simulation study confirms that our non-costly modification can lead to substantial improvements among Gaussian representations. We also compare it with three other established algorithms.

   @article{MR3881113,
     author = {Oesting, Marco and Strokorb, Kirstin},
     title = {Efficient simulation of {B}rown-{R}esnick processes based on
                   variance reduction of {G}aussian processes},
     journal = {Adv. in Appl. Probab.},
     fjournal = {Advances in Applied Probability},
     volume = {50},
     year = {2018},
     number = {4},
     pages = {1155--1175},
     issn = {0001-8678,1475-6064},
     mrclass = {60G70 (60G15 60G60)},
     mrnumber = {3881113},
     mrreviewer = {Ou\ Zhao},
     doi = {10.1017/apr.2018.54},
     url = {https://doi.org/10.1017/apr.2018.54}
   }

2017

1. Adv. Appl. Probab.

   

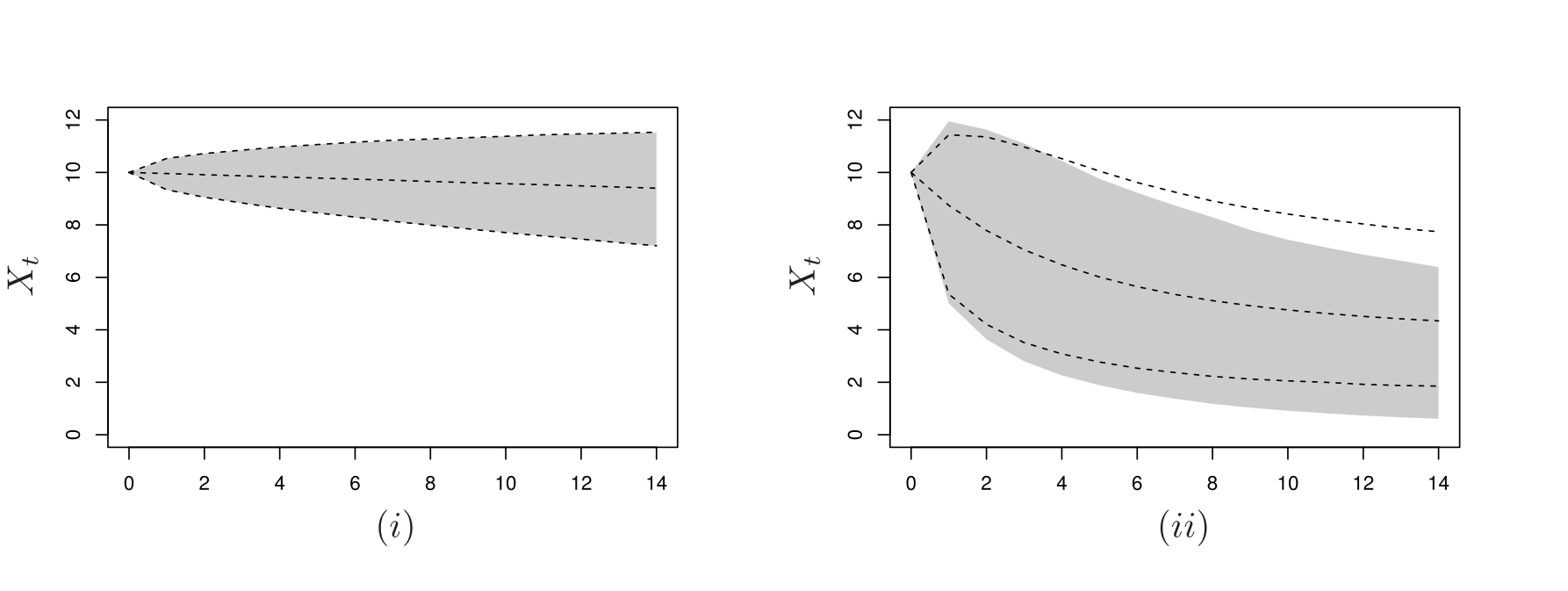   Extreme events of Markov chains

   I. Papastathopoulos, K. Strokorb, J. A. Tawn, and A. Butler

   Adv. in Appl. Probab., 2017

   Abs DOI Bib

   The extremal behaviour of a Markov chain is typically characterized by its tail chain. For asymptotically dependent Markov chains existing formulations fail to capture the full evolution of the extreme event when the chain moves out of the extreme tail region and for asymptotically independent chains recent results fail to cover well-known asymptotically independent processes such as Markov processes with a Gaussian copula between consecutive values. We use more sophisticated limiting mechanisms that cover a broader class of asymptotically independent processes than current methods, including an extension of the canonical Heffernan-Tawn normalization scheme, and reveal features which existing methods reduce to a degenerate form associated with non-extreme states.

   @article{MR3631219,
     author = {Papastathopoulos, I. and Strokorb, K. and Tawn, J. A. and Butler, A.},
     title = {Extreme events of {M}arkov chains},
     journal = {Adv. in Appl. Probab.},
     fjournal = {Advances in Applied Probability},
     volume = {49},
     year = {2017},
     number = {1},
     pages = {134--161},
     issn = {0001-8678,1475-6064},
     mrclass = {60G70 (60G10 60J05)},
     mrnumber = {3631219},
     mrreviewer = {Xin\ Thomson\ Tong},
     doi = {10.1017/apr.2016.82},
     url = {https://doi.org/10.1017/apr.2016.82}
   }

2. Extremes

   

   The realization problem for tail correlation functions

   Ulf-Rainer Fiebig, Kirstin Strokorb, and Martin Schlather

   Extremes, 2017

   Abs DOI Bib

   For a stochastic process {X_t}_t ∈T with identical one-dimensional margins and upper endpoint \tau_up its tail correlation function (TCF) is defined through χ^(X)(s,t)=lim_τ\to \tau_up P(X_s>τ|X_t> τ). It is a popular bivariate summary measure that has been frequently used in the literature in order to assess tail dependence. In this article, we study its realization problem. We show that the set of all TCFs on T \times T coincides with the set of TCFs stemming from a subclass of max-stable processes and can be completely characterized by a system of affine inequalities. Basic closure properties of the set of TCFs and regularity implications of the continuity of χare derived. If T is finite, the set of TCFs on T\times T forms a convex polytope of |T|\times |T| matrices. Several general results reveal its complex geometric structure. Up to |T|=6 a reduced system of necessary and sufficient conditions for being a TCF is determined. None of these conditions will become obsolete as |T| ≥3 grows.

   @article{MR3608783,
     author = {Fiebig, Ulf-Rainer and Strokorb, Kirstin and Schlather, Martin},
     title = {The realization problem for tail correlation functions},
     journal = {Extremes},
     fjournal = {Extremes. Statistical Theory and Applications in Science,
                   Engineering and Economics},
     volume = {20},
     year = {2017},
     number = {1},
     pages = {121--168},
     issn = {1386-1999,1572-915X},
     mrclass = {60G70 (52B05 52B12 60G52)},
     mrnumber = {3608783},
     mrreviewer = {Holger\ Drees},
     doi = {10.1007/s10687-016-0250-8},
     url = {https://doi.org/10.1007/s10687-016-0250-8}
   }

2016

1. SPA

   

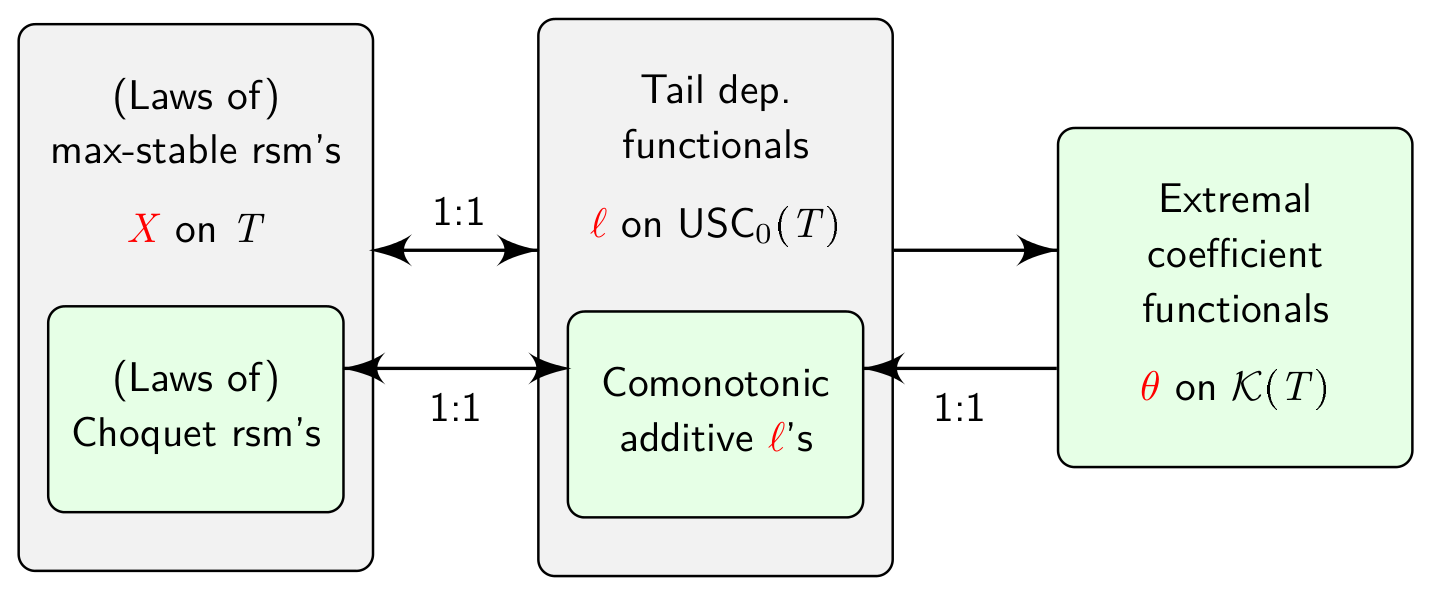   Max-stable random sup-measures with comonotonic tail dependence

   Ilya Molchanov and Kirstin Strokorb

   Stochastic Process. Appl., 2016

   Abs DOI Bib

   Several objects in the Extremes literature are special instances of max-stable random sup-measures. This perspective opens connections to the theory of random sets and the theory of risk measures and makes it possible to extend corresponding notions and results from the literature with streamlined proofs. In particular, it clarifies the role of Choquet random sup-measures and their stochastic dominance property. Key tools are the LePage representation of a max-stable random sup-measure and the dual representation of its tail dependence functional. Properties such as complete randomness, continuity, separability, coupling, continuous choice, invariance and transformations are also analysed.

   @article{MR3522303,
     author = {Molchanov, Ilya and Strokorb, Kirstin},
     title = {Max-stable random sup-measures with comonotonic tail
                   dependence},
     journal = {Stochastic Process. Appl.},
     fjournal = {Stochastic Processes and their Applications},
     volume = {126},
     year = {2016},
     number = {9},
     pages = {2835--2859},
     issn = {0304-4149,1879-209X},
     mrclass = {60G70 (28A12 60D05 60G57 91B16)},
     mrnumber = {3522303},
     mrreviewer = {Michael\ Falk},
     doi = {10.1016/j.spa.2016.03.004},
     url = {https://doi.org/10.1016/j.spa.2016.03.004}
   }

2. Stat. Probab. Lett.

   

   Conditional independence among max-stable laws

   Ioannis Papastathopoulos and Kirstin Strokorb

   Statist. Probab. Lett., 2016

   Abs DOI Bib

   Let X be a max-stable random vector with positive continuous density. It is proved that the conditional independence of any collection of disjoint sub-vectors of X given the remaining components implies their joint independence. We conclude that a broad class of tractable max-stable models cannot exhibit an interesting Markov structure.

   @article{MR3420420,
     author = {Papastathopoulos, Ioannis and Strokorb, Kirstin},
     title = {Conditional independence among max-stable laws},
     journal = {Statist. Probab. Lett.},
     fjournal = {Statistics \& Probability Letters},
     volume = {108},
     year = {2016},
     pages = {9--15},
     issn = {0167-7152,1879-2103},
     mrclass = {60G70 (62H05)},
     mrnumber = {3420420},
     mrreviewer = {Fabrizio\ Durante},
     doi = {10.1016/j.spl.2015.08.008},
     url = {https://doi.org/10.1016/j.spl.2015.08.008}
   }

2015

1. Extremes

   

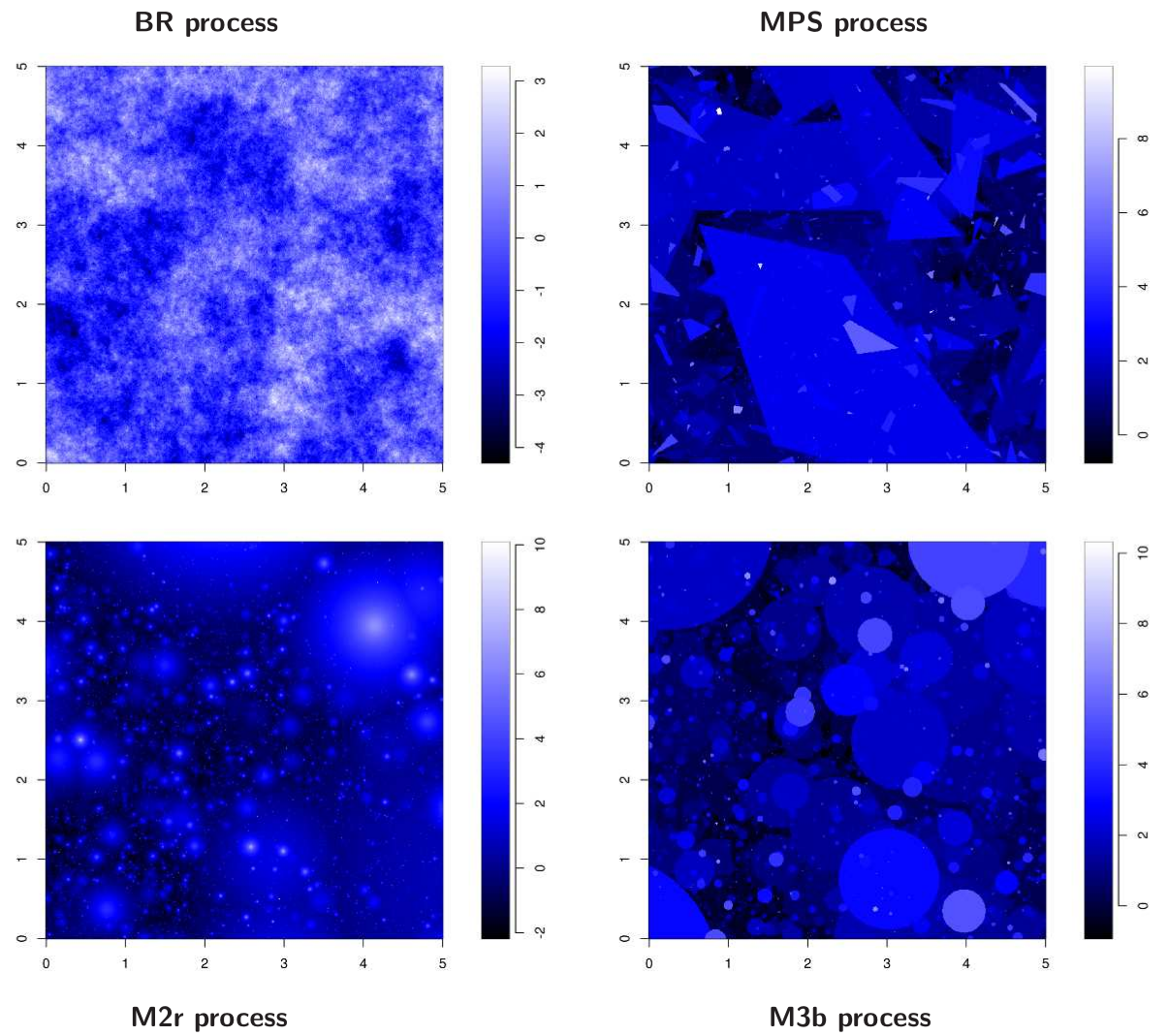   Tail correlation functions of max-stable processes: construction principles, recovery and diversity of some mixing max-stable processes with identical TCF

   Kirstin Strokorb, Felix Ballani, and Martin Schlather

   Extremes, 2015

   Abs DOI Bib

   The tail correlation function (TCF) is a popular bivariate extremal dependence measure to summarize data in the domain of attraction of a max-stable process. For the class of TCFs, being largely unexplored so far, several aspects are contributed: (i) generalization of some mixing max-stable processes (ii) transfer of two geostatistical construction principles to max-stable processes, including the turning bands operator (iii) identification of subclasses of TCFs, including M3 processes based on radial monotone shapes (iv) recovery of subclasses of max-stable processes from TCFs (v) parametric classes (iv) diversity of max-stable processes sharing an identical TCF. We conclude that caution should be exercised when using TCFs for statistical inference.

   @article{MR3351816,
     author = {Strokorb, Kirstin and Ballani, Felix and Schlather, Martin},
     title = {Tail correlation functions of max-stable processes:
                   construction principles, recovery and diversity of some mixing
                   max-stable processes with identical {TCF}},
     journal = {Extremes},
     fjournal = {Extremes. Statistical Theory and Applications in Science,
                   Engineering and Economics},
     volume = {18},
     year = {2015},
     number = {2},
     pages = {241--271},
     issn = {1386-1999,1572-915X},
     mrclass = {60G70 (60G52 60G60)},
     mrnumber = {3351816},
     mrreviewer = {Yizao\ Wang},
     doi = {10.1007/s10687-014-0212-y},
     url = {https://doi.org/10.1007/s10687-014-0212-y}
   }

2. Bernoulli

   

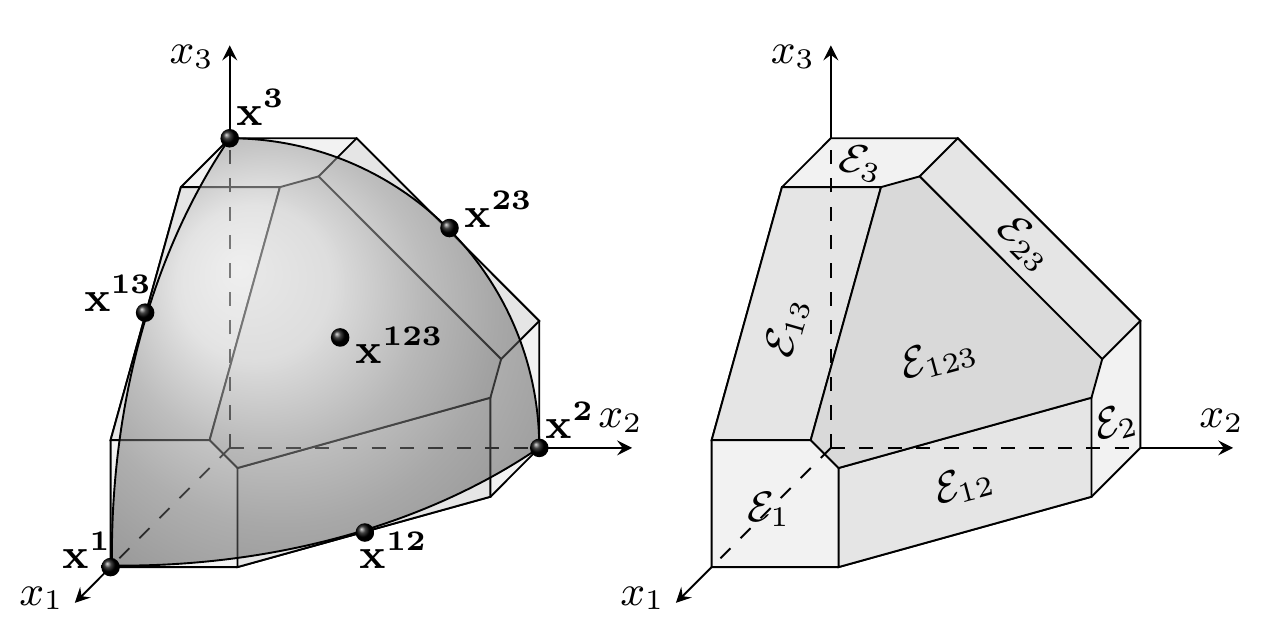   An exceptional max-stable process fully parameterized by its extremal coefficients

   Kirstin Strokorb and Martin Schlather

   Bernoulli, 2015

   Abs DOI Bib

   The extremal coefficient function (ECF) of a max-stable process X on some index set T assigns to each finite subset A ⊂T the effective number of independent random variables among the collection {X_t}_t ∈A. We introduce the class of Tawn-Molchanov processes that is in a 1:1 correspondence with the class of ECFs, thus also proving a complete characterization of the ECF in terms of negative definiteness. The corresponding Tawn-Molchanov process turns out to be exceptional among all max-stable processes sharing the same ECF in that its dependency set is maximal w.r.t. inclusion. This entails sharp lower bounds for the finite dimensional distributions of arbitrary max-stable processes in terms of its ECF. A spectral representation of the Tawn-Molchanov process and stochastic continuity are discussed. We also show how to build new valid ECFs from given ECFs by means of Bernstein functions.

   @article{MR3322319,
     author = {Strokorb, Kirstin and Schlather, Martin},
     title = {An exceptional max-stable process fully parameterized by its
                   extremal coefficients},
     journal = {Bernoulli},
     fjournal = {Bernoulli. Official Journal of the Bernoulli Society for
                   Mathematical Statistics and Probability},
     volume = {21},
     year = {2015},
     number = {1},
     pages = {276--302},
     issn = {1350-7265,1573-9759},
     mrclass = {60G70 (60G07)},
     mrnumber = {3322319},
     mrreviewer = {Sebastian\ Engelke},
     doi = {10.3150/13-BEJ567},
     url = {https://doi.org/10.3150/13-BEJ567}
   }

3. JSS

   

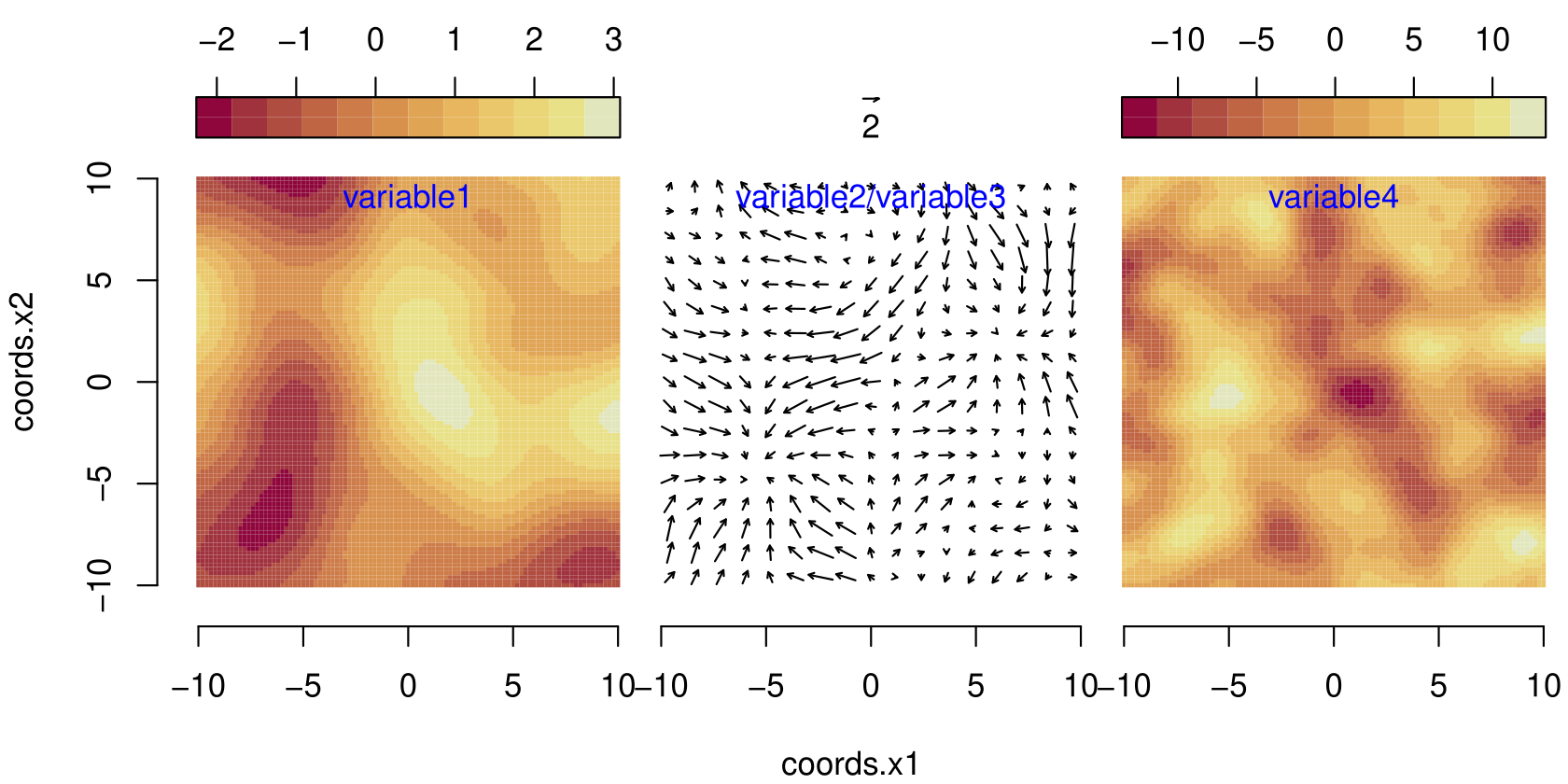   Analysis, Simulation and Prediction of Multivariate Random Fields with Package RandomFields

   Martin Schlather, Alexander Malinowski, Peter J. Menck, Marco Oesting, and Kirstin Strokorb

   J. Stat. Softw., 2015

   Abs DOI Bib

   Modeling of and inference on multivariate data that have been measured in space, such as temperature and pressure, are challenging tasks in environmental sciences, physics and materials science. We give an overview over and some background on modeling with crosscovariance models. The R package RandomFields supports the simulation, the parameter estimation and the prediction in particular for the linear model of coregionalization, the multivariate Matérn models, the delay model, and a spectrum of physically motivated vector valued models. An example on weather data is considered, illustrating the use of RandomFields for parameter estimation and prediction.

   @article{JSSv063i08,
     title = {Analysis, Simulation and Prediction of Multivariate Random Fields with Package RandomFields},
     volume = {63},
     url = {https://www.jstatsoft.org/index.php/jss/article/view/v063i08},
     doi = {10.18637/jss.v063.i08},
     number = {8},
     journal = {J. Stat. Softw.},
     fjournal = {Journal of Statistical Software},
     author = {Schlather, Martin and Malinowski, Alexander and Menck, Peter J. and Oesting, Marco and Strokorb, Kirstin},
     year = {2015},
     pages = {1–25}
   }

book chapters

2026

1. 

   Max-Stable Processes for Spatial Extremes

   Kirstin Strokorb and Marco Oesting

   In Handbook on Statistics of Extremes (to appear), 2026

   Abs Bib

   Max-stable processes are an analogue of max-stable distributions in a spatial setting. They are a mathematically motivated limiting process used to approximate block-maxima in time over space. In this capacity, they have become a first benchmark when answering questions on extremes that have a geostatistical nature. We summarize major developments of the last decades, covering theoretical properties, models and tools for inference. An indicative application demonstrates practical uses alongside hints where caution is needed. We close with some concluding remarks.

   @incollection{handbook-max-stab,
     author = {Strokorb, Kirstin and Oesting, Marco},
     title = {Max-Stable Processes for Spatial Extremes},
     booktitle = {Handbook on Statistics of Extremes (to appear)},
     series = {Chapman \& Hall/CRC Handb. Mod. Stat. Methods},
     publisher = {CRC Press, Boca Raton, FL},
     year = {2026}
   }

2. 

   Space-Time Modelling of Extremes

   Marco Oesting and Kirstin Strokorb

   In Handbook on Statistics of Extremes (to appear), 2026

   Abs Bib

   This chapter deals with statistical models to capture both spatial and temporal features of extreme events. We revisit general approaches to construct spatio-temporal models borrowing ideas from traditional geostatistics. Based on extensions of the models studied in Chapters 15-17, we consider asymptotically dependent models for maxima and threshold exceedances in space-time as well as more flexible subasymptotic models. We conclude with a brief discussion on further potential extensions and future developments in spatio-temporal modeling.

   @incollection{handbook-space-time,
     author = {Oesting, Marco and Strokorb, Kirstin},
     title = {Space-Time Modelling of Extremes},
     booktitle = {Handbook on Statistics of Extremes (to appear)},
     series = {Chapman \& Hall/CRC Handb. Mod. Stat. Methods},
     publisher = {CRC Press, Boca Raton, FL},
     year = {2026}
   }

Theses

2013

1. PhD Thesis

   Characterization and construction of max-stable processes

   Kirstin Strokorb

   University of Göttingen, Institute for Mathematical Stochastics, 2013

   DOI

2010

1. Diplomarbeit

   Eine holomorphe Untersuchung des verallgemeinerten Seiberg-Witten-Modulraumes für Gibbons-Hawking-Faserungen

   Kirstin Strokorb

   Georg-August-Universität Göttingen, Mathematisches Institut, 2010

   HTML